№ 10.14 Геометрія = № 18.14 Математика
MN – середня лінія трапеції ABCD, яка перетинає діагональ AC у точці K. Знайдіть MK і KN, якщо основи трапеції дорівнюють 18 см і 12 см.
Розв'язок:
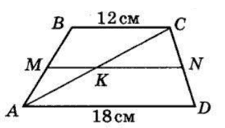
MN — середня лінія трапеції, MN || AD, MN || BC.
У ΔABC M — середина AB, MK || AD, тоді K — середина AC, MK — середня лінія ΔABC.
MK = $\frac{1}{2}$ BC = $\frac{1}{2}$ · 12 = 6 (см).
KN — середня лінія ΔACD,
KN = $\frac{1}{2}$ AD = $\frac{1}{2}$ · 18 = 9 (см).
Відповідь:
6 см, 9 см.
