№ 62 Геометрія = № 62 Математика
Пряма MK – дотична до кола, точка O – центр кола, точка M – точка дотику. Знайдіть ∠MOB, якщо ∠KMB = 70°.
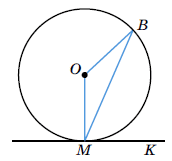
Розв'язок:
Дотична до кола є перпендикулярною до радіуса, який проведений в точку дотику (згідно властивості дотичної до кола), тому
∠OMK = 90°.
Тоді
∠OMB = ∠OMK − ∠BMK = 90° – 70° = 20°.
Трикутник OMB — рівнобедрений, оскільки OM = OB (радіуси кола).
Загальна властивість:
У рівнобедреному трикутнику кути при основі рівні (∠OBM = ∠OMB), а також сума всіх трьох кутів дорівнює 180°:
∠MOB + ∠OBM +∠OMB = 180°,
∠MOB + 20° + 20° = 180°,
∠MOB = 140°.
Відповідь:
∠MOB = 140°
