№ 60 Геометрія = № 60 Математика
На малюнку точка O – центр кола, ∠ACO = 21°. Знайдіть ∠COB.
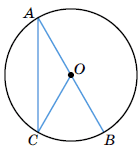
Розв'язок:
OC = OB (як радіуси), тому △ACO рівнобедрений. Оскільки у рівнобедреного трикутника кути при основі рівні, то ∠ACO = ∠CAO = 21°.
∠COB — центральний кут, що спирається на дугу CB, ∠CAB — вписаний кут, що також спирається на ту саму дугу CB.
Центральний кут вдвічі більший за вписаний, якщо вони спираються на одну й ту ж дугу (згідно теореми про вписаний кут):
∠COB = 2 ∙ ∠CAB = 2 ∙ 21° = 42°.
Відповідь:
∠COB = 42°.
