№ 40 Геометрія = № 40 Математика
На малюнку AB = BD, AC = CD. Доведіть, що BC – бісектриса кута ABD.
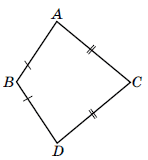
Розв'язок:
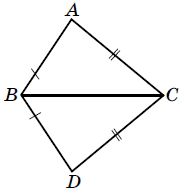
Розглянемо трикутники △ABC і △DBC:
BC — спільна сторона;
AB = BD — за умовою;
AC = CD — за умовою.
Отже, трикутники рівні за трьома сторонами (згідно з третьою ознакою рівності трикутників):
△ABC = △DBC.
Із рівності трикутників випливає, що відповідні кути також рівні:
∠ABC = ∠DBC ⇒ BC — бісектриса кута ∠ABD.
Відповідь:
✅ Доведено.
