№ 15 Геометрія = № 15 Математика
Знайдіть суміжні кути, якщо один з них:
1) удвічі більший за інший;
2) становить $\frac{2}{7}$ від іншого.
Розв'язок:
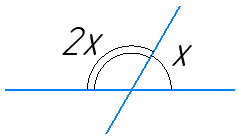
1) Нехай менший кут х, тоді більший — 2х. Сума суміжних кутів рівна 180°:
х + 2х = 180°
3х = 180°
х = 60° — менший кут
2х = 2 ∙ 60° = 120° — більший кут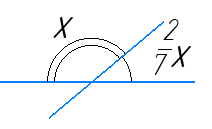
2) Нехай більший кут х, тоді менший — $\frac{2}{7}х.$ Сума суміжних кутів рівна 180°:
х + $\frac{2}{7}х = 180°$
$\frac{9}{7}х = 180°$
9х = 180° ∙ 7
х = 20° ∙ 7
х = 140°
$\frac{2}{7}х = \frac{2}{7}$ ∙ 140° = 2 ∙ 20° = 40°
Відповідь:
1) 60°, 120°;
2) 40°, 140°.
