№ 55 ЗПС Алгебра = № 55 ЗПС Математика
По двох взаємно перпендикулярних дорогах рухаються в напрямку перехрестя пішохід і велосипедист. У деякий момент часу пішохід знаходиться на відстані 2 км, а велосипедист – на відстані 3,75 км від перехрестя доріг. Через який час відстань між ними дорівнюватиме 1,25 км, якщо швидкість пішохода 5 км/год, а велосипедиста – 15 км/год?
Розв'язок:
Нехай через $x$ год відстань
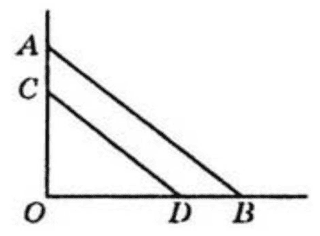
$CD=1{,}25$ км, $AO=2$ км;
$BO=3{,}75$ км; $CD=1{,}25$ км;
$AC=5x$ км; $OC=2-5x;$
$BD=15x$ км;
$OD=3{,}75-15x. $
За теоремою Піфагора
$OC^2+OD^2=CD^2.$
Маємо рівняння: $(2-5x)^2+(3{,}75-15x)^2=$
$= 1{,}{25}^2;$
$4-20x+25x^2+14{,}0625+$
$+ 225x^2-112{,}5x=1{,}5625;$
$250x^2-132{,}5x+16{,}5x=0;$
$2500x^2-1325x+165x=0;$
$500x^2-265x+33=0;$
$D=70\ 225-66\ 000=4225;$
$x_1=\frac{265+65}{1000}=\frac{330}{1000}=0{,}33;$
$x_2=\frac{265-65}{1000}=\frac{200}{1000}=0{,}2.$
Відповідь:
0,2 год або 0,33 год.
