№ 52 ЗПС Алгебра = № 52 ЗПС Математика
З міста A в місто B, відстань між якими 164 км, зі швидкістю 20 км/год виїхав велосипедист. Через 2 год у тому самому напрямку виїхав мотоцикліст, який, обігнавши велосипедиста, прибув у місто B і одразу повернув назад. Знайдіть швидкість мотоцикліста, якщо він зустрів велосипедиста через 2 год 45 хв після того, як його обігнав.
Розв'язок:
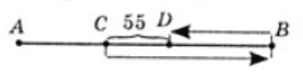
Нехай C – пункт, в якому мотоцикліст обігнав велосипедиста, D- пункт, в якому мотоцикліст зустрів велосипедиста, повертаючись назад; $x$ год – час, за який велосипедист подолав відстань AD, тоді $(x-2)$ год – час, який був у дорозі мотоцикліст.
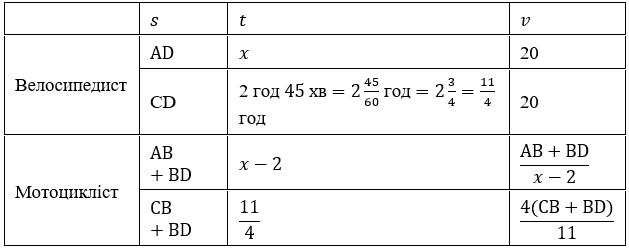
$AD=20x;$
$CD=AB-AD=$
$= 164-20x;$
$AB+BD= 164+164-$
$- 20x= 328-20x;$
$CB+BD= 55+164-20x+$
$+ 164-20x= 55+328-$
$- 40x= 383-40x.$
Маємо рівняння:
$\frac{AB+BD}{x-2}=\frac{4(CB+BD)}{11};$
$\frac{328-20x}{x-2}=\frac{4(328-10x)}{11};$
$\frac{82-5x}{x-2}=\frac{383-40x}{11};$
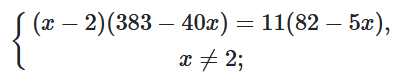
$383x-766-40x^2+80x=$
$= 902-55x;$
$40x^2-518x+1668=0;$
$ 20x^2-259x+834=0;$
$D=67081-66720=361;$
$x_1=\frac{259+19}{40}=6{,}95;$
$x_1=\frac{259-19}{40}=\frac{240}{40}=6.$
$\frac{AB+BD}{x-2}=\frac{328-20x}{x-2}=$
$= \frac{328-20\cdot6,95}{6,95-2}=\frac{328-139}{4,95}=$
$= \frac{189}{4,95}=\frac{18\ 900}{495}=$
$= \frac{3780}{99}=\frac{420}{11}=38\frac{2}{11}$ (км/год)
