№ 45 ЗПС Алгебра = № 45 ЗПС Математика
Розв’яжіть рівняння:
1. $\frac{x-3}{x-1}+\frac{x+3}{x+1}=\frac{x+6}{x+2}+\frac{x-6}{x-2};$
2. $\frac{x-2}{x-1}+\frac{x+2}{x+1}+\frac{28}{15}=$
$= \frac{x-4}{x-3}+ \frac{x+4}{x+3}.$
Розв'язок:
1. $\frac{x-3}{x-1}+\frac{x+3}{x+1}=\frac{x+6}{x+2}+\frac{x-6}{x-2};$
$\frac{(x-3)(x+1)+(x+3)(x-1)}{(x-1)(x+1)}=$
$= \frac{(x+6)(x-2)+(x-6)(x+2)}{(x+2)(x-2)};$
$\frac{x^2+x-3x-3+x^2+3x-x-3}{x^2-1}=$
$= \frac{x^2+6x-2x-12+x^2-6x+2x-12}{x^2-4};$
$\frac{2x^2-6}{x^2-1}=\frac{2x^2-24}{x^2-4};$
$\frac{2x^2-6}{x^2-1}-\frac{2x^2-24}{x^2-4}=0;$
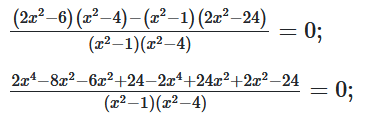
$\left\{\begin{matrix}12x^2=0;\\x\neq-1,x\neq1,\\x\neq-2,x\neq2;x=0.\\\end{matrix}\right.$
2. $\frac{x-2}{x-1}+\frac{x+2}{x+1}+\frac{28}{15}=$
$= \frac{x-4}{x-3}+ \frac{x+4}{x+3}.$
$\frac{\left(x+3\right)\left(x-4\right)+\left(x-3\right)\left(x+4\right)}{\left(x-3\right)\left(x+3\right)}-$
$- \frac{\left(x-1\right)\left(x-2\right)+\left(x-1\right)\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}=\frac{28}{15};$
$\frac{x^2-x-12+x^2+x-12}{x^2-9}-$
$- \frac{x^2-x-2+x^2+x-2}{x^2-1}=\frac{28}{15};$
$\frac{2x^2-24}{x^2-9}-\frac{2x^2-4}{x^2-1}=\frac{28}{15};$
$\frac{\left(2x^2-24\right)\left(x^2-1-\left(2x^2-4\right)\left(x^2-9\right)\right.}{\left(x^2-9\right)\left(x^2-1\right)}=$
$= \frac{28}{15};$
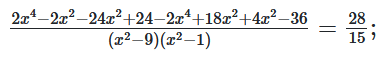
$\frac{-4x^2-12}{\left(x^2-9\right)\left(x^2-1\right)}=\frac{28}{15};$
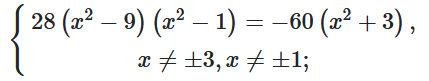
$7\left(x^2-9\right)\left(x^2-1\right)=$
$= -15\left(x^2+3\right);$
$7\left(x^4-x^2-9x^2+9\right)=$
$= -15x^2-45;$
$7x^4-70x^2+63+15x^2+$
$+ 45=0;$
$7x^4-55x^2+108=0.$
Нехай $x^2=t≥0,$ тоді
$x^4=t^2.\ 7t^2-55t+108=0.$
$D=(-55)^2-4·7·108=$
$= 3025-3024=1;$
$t_1=\frac{55+1}{14}=\frac{56}{14}=\frac{8}{2}=4;$
$t_2=\frac{55-1}{14}=\frac{54}{14}=\frac{27}{7}.$
$\left[\begin{matrix}x^2=4,\\x^2=\frac{27}{7};x=\pm2;\\\end{matrix}\right.$
$x=\pm\frac{\sqrt{27}}{\sqrt7}=\pm\frac{9\sqrt3}{\sqrt7}=\pm\frac{9\sqrt{21}}{7}.$
Відповідь:
1. $0;$
2. $-2;2;-\frac{9\sqrt{21}}{7};\frac{9\sqrt{21}}{7}.$
