Завдання № 43

№ 43 ЗПС Алгебра = № 43 ЗПС Математика

Спростіть вираз:

1. $(\frac{1}{x^2+3x+2}+\frac{2x}{x^2+4x+3}+$

$+ \frac{1}{x^2+5x+6})^2\cdot\frac{(x-3)^2+12x}{2}.$

2. $\frac{3a^2+2ab-b^2}{a^2+4ab+3b^2}-2+\frac{10(ab-3b^2)}{a^2-9b^2}.$

Розв'язок:

1. $(\frac{1}{x^2+3x+2}+\frac{2x}{x^2+4x+3}+$

$+ \frac{1}{x^2+5x+6})^2\cdot\frac{(x-3)^2+12x}{2}=2;$

а) $\frac{1}{x^2+3x+2}+\frac{2x}{x^2+4x+3}+\frac{1}{x^2+5x+6}=$

$= \frac{1}{(x+2)(x+1)}+\frac{2x}{(x+3)(x+1)}+$

$+ \frac{1}{(x+2)(x+3)}=$

$= \frac{x+3+2x(x+2)+x+1}{(x+1)(x+2)(x+3)}=$

$= \frac{x+3+2x^2+4x+x+1}{(x+1)(x+2)(x+3)}=$

$= \frac{2x^2+6x+4}{(x+1)(x+2)(x+3)}=$

$= \frac{2\left(x^2+3x+2\right)}{(x+1)(x+2)(x+3)}=$

$= \frac{2(x+2)(x+1)}{(x+1)(x+2)(x+3)}=\frac{2}{x+3};$

б) $\left(\frac{2}{x+3}\right)^2\cdot\frac{(x-3)^2+12x}{2}=$

$= \frac{4\cdot\left(x^2+6x+9\right)}{2\cdot(x+3)^2}= \frac{4(x+3)^2}{2(x+3)^2}=2;$

2. $\frac{3a^2+2ab-b^2}{a^2+4ab+3b^2}-2+\frac{10\left(ab-3b^2\right)}{a^2-9b^2}=$

$= \frac{3a^2+2ab-b^2}{\left(a^2+4ab+4b^2\right)-b^2}-2+$

$+ \frac{10b(a-3b)}{(a-3b)(a+3b)}=$

$= \frac{3a^2+2ab-b^2}{(a+2b)^2-b^2}-2+\frac{10b}{a+3b}=$

$= \frac{3a^2+2ab-b^2}{(a+2b-b)(a+2b+b)}-2+\frac{10b}{a+3b}=$

$= \frac{3a^2+2ab-b^2}{(a+b)(a+3b)}-2+\frac{10b}{a+3b}=$

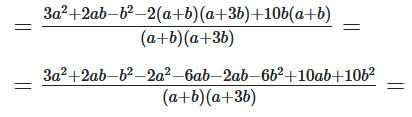
$= \frac{a^2+3b^2+4ab}{(a+b)(a+3b)}=\frac{a^2+3b^2+4ab}{a^2+3ab+ab+3b^2}=$

$= \frac{a^2+3b^2+4ab}{a^2+3b^2+4ab}=1.$