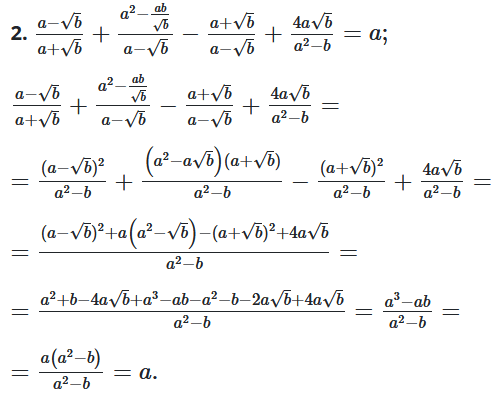№ 24 ЗПС Алгебра = № 24 ЗПС Математика
Доведіть тотожність:
1. $\left(1+\sqrt{1-x^2}+\frac{x^2}{\sqrt{1-x^2}}\right):$
$: \left(\frac{1}{1-x^2}+\frac{1}{\sqrt{1-x^2}}\right)=$
$= \sqrt{1-x^2};$
2. $\frac{a-\sqrt b}{a+\sqrt b}+\frac{a^2-\frac{ab}{\sqrt b}}{a-\sqrt b}-\frac{a+\sqrt b}{a-\sqrt b}+$
$+ \frac{4a\sqrt b}{a^2-b}=a.$
Розв'язок:
1. $\left(1+\sqrt{1-x^2}+\frac{x^2}{\sqrt{1-x^2}}\right):$
$: \left(\frac{1}{1-x^2}+\frac{1}{\sqrt{1-x^2}}\right)=\sqrt{1-x^2};$
a) $ 1+\sqrt{1-x^2}+\frac{x^2}{\sqrt{1-x^2}}=$
$= \frac{\sqrt{1-x^2}+x^2+1-x^2}{\sqrt{1-x^2}}= \frac{\sqrt{1-x^2}+1}{\sqrt{1-x^2}};$
б) $ \frac{1}{1-x^2}+\frac{1}{\sqrt{1-x^2}}=$
$= \frac{1}{1-x^2}+\frac{\sqrt{1-x^2}}{1-x^2}= \frac{1+\sqrt{1-x^2}}{1-x^2};$
в) $\frac{\sqrt{1-x^2}+1}{\sqrt{1-x^2}}:\frac{1+\sqrt{1-x^2}}{1-x^2}=$
$= \frac{\sqrt{1-x^2}+1}{\sqrt{1-x^2}}\cdot\frac{1-x^2}{1+\sqrt{1-x^2}}=$
$= \frac{1-x^2}{\sqrt{1-x^2}}=\frac{\left(1-x^2\right)\sqrt{1-x^2}}{1-x^2}=$
$= \sqrt{1-x^2}; $