ВПР 3 №66 Алгебра = ВПТ 11 №34 Математика
З міст A і B одночасно назустріч один одному виїхали два велосипедисти і зустрілися через 5 год. Швидкість велосипедиста, який виїхав з міста A, на 5 км/год менша від швидкості другого велосипедиста. Якби другий велосипедист виїхав на 4,5 год пізніше, ніж перший, то вони зустрілися б на відстані 75 км від міста B. Знайдіть відстань між містами A і B.
Розв'язок:
Нехай $x$ км/год – швидкість велосипедиста, що виїхав з пункту B, тоді $(x-5)$ км/год – швидкість велосипедиста, що виїхав з пункту A. Відстань між містами A і B становить
$5x+5(x-5)=$
$= 5x+5x-25=$
$= 10x-25. $
Маємо рівняння:
$\frac{10x-25-75}{x-5}-\frac{75}{x}=\frac{9}{2};$
$\frac{10x-100}{x-5}-\frac{75}{x}=\frac{9}{2};$
$\frac{x(10x-100)-75(x-5)}{x(x-5)}=\frac{9}{2};$
$\frac{10x^2-100x-75x+375}{x(x-5)}=\frac{9}{2};$
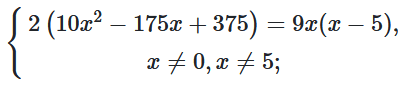
$20x^2-350x+750-9x^2+$
$+ 45x=0;$
$11x^2-305x+750=0;$
$D=(-305)^2-4·11·750=$
$= 93\ 025-33\ 000=60\ 025=2452; $
$x_1=\frac{305+245}{22}=\frac{550}{22}=25;$
$x_2=\frac{305-245}{22}=\frac{60}{22}=\frac{30}{11}=$
$= 2\frac{8}{11}<5$ (умові задачі не задовольняє).
AB = $10x-25=10·25-25=$
$= 250-25=225$ (км).
Відповідь:
225 км.
