ВПР 3 №54 Алгебра = ВПТ 11 №22 Математика
Знайдіть корені рівняння:
1. $\left(x^2-4x\right)(x-2)^2+3=0;$
2. $x\left(x-1\right)\left(x-2\right)\left(x-3\right)=24;$
3. $x^2-3x=\frac{8}{x^2-3x-2};$
4. $(x+2)(x-7)=\frac{19}{(x-1)(x-4)};$
5. $\frac{5}{x^2-x-1}+\frac{1}{x^2-x-5}=2;$
6. $\frac{2}{x^2-11x+4}+\frac{3}{x^2-11x+1}=$
$= \frac{8}{x^2-11x-2}.$
Розв'язок:
1. $\left(x^2-4x\right)(x-2)^2+3=0;$
$\left(x^2-4x\right)\left(x^2-4x+4\right)+$
$+ 3=0.$
Нехай $x^2-4x=t,$
тоді $t(t+4)+4=0;$
$t^2+4t+3=0;$
$t_1=-3;t_2=-1.$
Отже, $\left[\begin{matrix}x^2-4x=-3,\\x^2-4x=-1;\\\end{matrix}\right.$
$\left[\begin{matrix}x^2-4x+3=0,\\x^2-4x+1=0;\\\end{matrix}\right.$
1) $x^2-4x+3=0;$
$x_1=1;x_2=3;$
2) $x^2-4x+1=0;$
$D=(-4)^2-4·1·1=$
$= 16-4=12;$
$x_1=\frac{4+\sqrt{12}}{2}=\frac{4+2\sqrt3}{2}=$
$= \frac{2(2+\sqrt3)}{2}=2+\sqrt3;$
$x_2=2-\sqrt3.$
2. $x\left(x-1\right)\left(x-2\right)\left(x-3\right)=$
$= 24;$
$\left(x-3\right)\left(x-1\right)\left(x-2\right)=24;$
$\left(x^2-3x\right)\left(x^2-3x+2\right)=24.$
Нехай $x^2-3x=t,$
тоді $t(t+2)-24=0;$
$t^2+2t-24=0;$
$t_1=-6;t_2=4.$
$\left[\begin{matrix}x^2-3x=-6,\\x^2-3x=4; \\\end{matrix}\right.$
$\left[\begin{matrix}x^2-3x+6=0, \\ x^2-3x-4=0; \\\end{matrix} \right.$
(коренів немає, бо $D<0$); $x_1=4;x_2=-1.$
3. $x^2-3x=\frac{8}{x^2-3x-2};$
$x^2-3x\neq0.$
Нехай $x^2-3x=t,$ тоді
$\frac{8}{t-2}=t;$
$\left\{\begin{matrix}t(t-2)=0,\\t\neq2;\\\end{matrix}\right.$
$t^2-2t-8=0;$
$t_1=4;t_2=-2.$
$\left[\begin{matrix}x^2-3x=4,\\x^2-3x=-2;\\\end{matrix}\right.$
$\left[\begin{matrix}x^2-3x-4=0,\\x^2-3x+2=0;\\\end{matrix}\right.$
1) $x^2-3x-4=0;$
$x_1=4;x_2=-1;$
2) $x^2-3x+2=0;$
$x_1=1;x_2=2.$
4. $(x+2)(x-7)=\frac{19}{(x-1)(x-4)};$
$x^2-5x-14=\frac{19}{x^2-5x+4};$
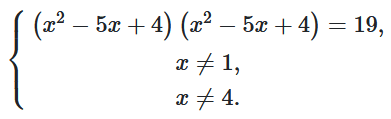
Нехай $x^2-5x+4=t,$ тоді
$\left.t-18=\frac{19}{t}\right|\ \cdot t;$
$(t-14)(t+4)=0;$
$t^2-18t-56=19;$
$t^2-10t-75=0;$
$D=(-10)^2-4·1·(-75)=$
$= 100+300=400;$
$t_1=\frac{10+20}{2}=\frac{30}{2}=15;$
$t_1=\frac{10-20}{2}=-5;$
$\left[\begin{matrix}x^2-5x=15,\\x^2-5x=-5;\\\end{matrix}\right.$
$\left[\begin{matrix}x^2-5x-15=0,\\x^2-5x+5=0;\\\end{matrix}\right.$
1) $x^2-5x-5=0;$
$D=(-5)^2-4·1·(-15)=$
$= 25+60=85;$
$x_1=\frac{5+\sqrt{85}}{2};$
$x_2=\frac{5-\sqrt{85}}{2};$
2) $x^2-5x+5=0;$
$D=(-5)^2-4·5=$
$= 25-20=5;$
$x_3=\frac{5+\sqrt5}{2};$
$x_4=\frac{5-\sqrt5}{2}.$
5. $\frac{5}{x^2-x-1}+\frac{1}{x^2-x-5}=2.$
Нехай $x^2-x=t,$ тому
$\frac{5}{t-1}+\frac{1}{t-5}=2;$
$\frac{5(t-5)+t-1}{(t-1)(t-5)}=\frac{2}{1};$
$\frac{6t-26}{t-6t+5}=\frac{2}{1};$
$\left\{\begin{matrix}29t^2-6t+5=6t-26,\\t\neq1,\\t\neq5;\\\end{matrix}\right.$
$2t^2-12t+10-6t+26=0;$
$2t^2-18t+36=0;$
$t^2-9t+18=0;$
$t_1=4; t_2=-2.$
$\left[\begin{matrix}x^2-x=3,\\x^2-x=6;\\\end{matrix}\right.$
$\left[\begin{matrix}x^2-x-3=0,\\x^2-x-6=0;\\\end{matrix}\right.$
1) $x^2-x-6=0;$
$D=(-1)^2-4·(-3)=$
$= 1+12=13;$
$x_1=\frac{1+\sqrt{13}}{2};$
$x_2=\frac{1-\sqrt{13}}{2};$
2) $x^2-x-6=0;$
$x_1=3;x_2=-2.$
6. $\frac{2}{x^2-11x+4}+\frac{3}{x^2-11x+1}=$
$= \frac{8}{x^2-11x-2}.$
Нехай $x^2-11x=t,$ тоді
$\frac{2}{t+4}+\frac{3}{t+1}-\frac{8}{t-2}=0;$
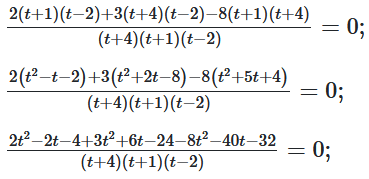
$\frac{-3t^2-36t-60}{(t+4)(t+1)(t-2)}=0;$
$\left[\begin{matrix}3t^2-36t-60=0,\\t\neq-4,\\t\neq-1,\\t\neq2;\\\end{matrix}\right.$
$t^2+12t+20=0;$
$D={12}^2-4·1·20=$
$= 144-80=64;$
$t_1=\frac{-12+8}{2}=-\frac{4}{2}=-2;$
$t_2=\frac{-12-8}{2}=-\frac{20}{2}=-10;$
$\left[\begin{matrix}x^2-11x=-2\\x^2-11x=-10;\\\end{matrix}\right.$
$\left[\begin{matrix}x^2-11x+2=0;\\x^2-11x+10=0;\\\end{matrix}\right.$
1) $x^2-11x+2=0;$
$D=(-11)^2-4·1·2=$
$= 121-8=113;$
$x_1=\frac{11+\sqrt{113}}{2};$
$x_2=\frac{11-\sqrt{113}}{2};$
2) $x^2-11x+10=0;$
$D=(-11)^2-4·1·10=$
$= 121-40=81;$
$x_3=\frac{11+9}{2}=\frac{20}{2}=10;$
$x_1=\frac{11-9}{2}=\frac{2}{2}=1.$
Відповідь:
1. $1; 3;2\pm\sqrt3;$
2. $-1;4;$
3. $-1;1;2;4.$
4. $\frac{5\pm5\sqrt{85}}{2};\frac{5\pm\sqrt5}{2};$
5. $-2;3;\frac{1\pm\sqrt{13}}{2};$
6. $1;10;\frac{11\pm\sqrt{113}}{2}.$
