ВПР 3 №32 Алгебра = ВПТ 9 №32 Математика
Відкриту коробку об’ємом 10 500 см3 виготовили з аркуша картону прямокутної форми, довжина якого вдвічі більша за ширину, вирізавши з кутів аркуша квадрати зі стороною 5 см. Знайдіть початкові розміри аркуша.
Розв'язок:
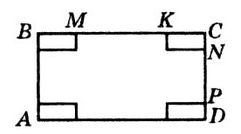
Нехай AB = 2x см, BC = 2x см, MK = 2x - 10 см, NP = x - 10 см,
тоді $V=(2x-10)(x-10)·5=$
$= 10\ 500;$
$(2x-10)(x-10)·5=$
$= 10\ 500:5;$
$(2x-10)(x-10)·5=2100;$
$2x^2-20x-10x+$
$+ 100-2100=0;$
$2x^2-30x-2000=0;$
$x^2-15x-1000=0.$
$D=(-15)^2-4·1(-1000)=$
$= 225+4000=4225;$
$x_1=\frac{15+65}{2}=\frac{80}{2}=40;$
$x_2=\frac{15-65}{2}<0$ (умові задачі не задовольняє).
$2x=40·2=80$ (см).
Відповідь:
40 см і 80 см.
