Завдання № 29

ВПР 3 №29 Алгебра =  ВПТ 9 №29 Математика

Один з катетів прямокутного трикутника на 2 см менший від другого, а периметр трикутника дорівнює 24 см. Знайдіть площу трикутника.

Розв'язок:

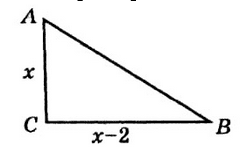
Нехай $AC=x,BC=x-2;$

$AB=24-\left(x+x-2\right)=$

$= 24-2x+2=26-2x.$

За теоремою Піфагора маємо:

$AB^2=AC^2+BC^2;$

$(26-2x)^2=x^2+(x-2)^2;$

$676-104x+4x^2=$

$= x^2+x^2-4x+4;$

$4x^2-2x^2-104x+4x+$

$+ 676-4=0;$

$2x^2-100x+672=0;$

$x^2-50x+336=0;$

$D=(-50)^2-4·1·336=$

$= 2500-1344=1156;$

$x_1=\frac{50+34}{2}=\frac{84}{2}=42$ (умові задачі не задовольняє, бо тоді $AB<0;$

$x_2=\frac{50-34}{2}=\frac{16}{2}=8.$

$x-2=8-2=6.$ Отже,

$S_{\triangle A C B}=\frac{AC\cdot BC}{2}=\frac{8\cdot6}{2}=$

$= 4\cdot6=$24см². 

Відповідь: 

24 см².