ВПР 3 №11 Алгебра = ВПТ 9 №11 Математика
Розв’яжіть рівняння графічно, а потім перевірте розв’язок аналітично:
1. $x^2=3-2x;$
2. $x^2=0{,}5x+3.$
Розв'язок:
1. Побудуємо в одній системі координат графіки функцій
$y=x^2$ та $y=3-2x. $
$y=x^2.$

$y=3-2x.$
| x | 0 | 1 |
| y | 3 | 1 |
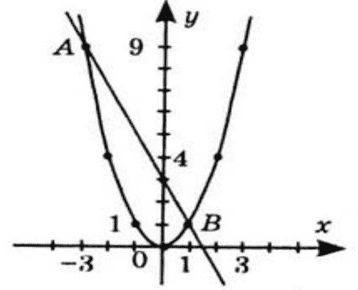
Точки $A\left(-3;9\right)$ та $B\left(1;1\right)$ – точки перетину графіків функцій
$y=x^2$ та $y=3-2x.$
Отже, $x=-3,x=1;$
$x^2+2x-3=0;$
$D=2^2-4·1·-3=$
$= 4+12=16;$
$x_1=\frac{-2+4}{2}=\frac{2}{2}=1;$
$x_2=\frac{-2-4}{2}=-\frac{6}{2}=-3.$
2. $x^2=0{,}5x+3.$
Побудуємо в одній системі координат графіки функцій
$y=x^2$ та $y=0{,}5x+3.$
$ y=x^2.$
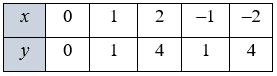
$y=0{,}5x+3.$
| x | 0 | 2 |
| y | 3 | 4 |
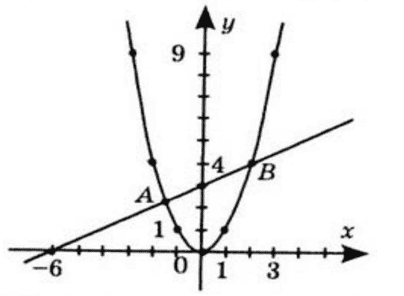
Точки $A(-1{,}5;2{,}25)$ та $B(2;4)$ – точки перетину графіків функцій
$y=x^2$ та $y=0{,}5x+3.$
Отже, $x_1=-1{,}5,x_2=2;$
$ x^2=0{,}5x+3;$
$x^2-0{,}5x-3=0;$
$10x^2-5x-30=0;$
$2x^2-x-6=0;$
$D=(-1)^2-4·2·(-6)=$
$= 1+48=49;$
$x_1=\frac{1+7}{2}=\frac{8}{4}=2;$
$x_2=\frac{1-7}{2}=-\frac{6}{4}=$
$= -\frac{3}{2}=-1{,}5.$
Відповідь:
1. $-3;1;$
2. $-1{,}5;2.$
