№ 26.7 Алгебра = № 51.7 Математика
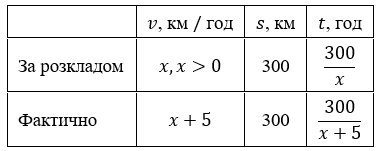
Щоб ліквідувати запізнення на 40 хв, поїзд на перегоні 300 км завдовжки збільшив швидкість на 5 км/год порівняно зі швидкістю за розкладом. Якою є швидкість поїзда за розкладом?
Розв'язок:
$40$xв = $\frac{40}{60}$ год = $\frac{2}{3}$ год;
$\frac{300}{x}>\frac{300}{x+5}$ (на $\frac{2}{3});$
$\frac{300}{x}-\frac{300}{x+5}=\frac{2}{3};$
$ \frac{300\left(x+5\right)-300x}{x\left(x+5\right)}=\frac{2}{3};$
$\frac{300x+1500-300x}{x(x+5)}=\frac{2}{3};$
$\frac{1500}{x(x+5)}=\frac{2}{3};$
$\left\{\begin{matrix}2x(x+5)=4500,\\x\neq0,\\x\neq0,x\neq-5;\\\end{matrix}\right.$
$2x^2+10x-4500=0;$
$x^2+5x-2250=0;$
$D=5^2-4·1·(-2250)=$
$= 25+9000=9025;$
$x_1=\frac{-5+95}{2}=\frac{90}{3}=45;$
$x_2=\frac{-5-95}{2}<0$ (умові задачі не задовольняє).
Відповідь:
45 км/год.
