№ 26.4 Алгебра = № 51.4 Математика
Знаменник звичайного нескоротного дробу на 5 більший за чисельник. Якщо знаменник збільшити на 6, а чисельник збільшити на 4, то дріб збільшиться на $\frac{1}{4}.$ Знайдіть цей дріб.
Розв'язок:
Нехай $\frac{x}{x+5}$ – даний звичайний нескоротний дріб, тоді
$\frac{x+4}{x+5+6}=\frac{x}{x+5}+\frac{1}{4};$
$\frac{x+4}{x+11}-\frac{x}{x+5}-\frac{1}{4}=0;$
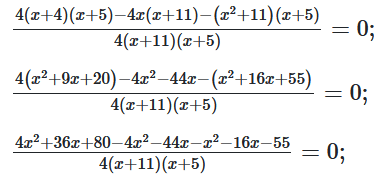
$\frac{-x^2-24x+25}{4(x+11)(x+5)}=0;$
$\left\{\begin{matrix}x^2+24x-25=0,\\x\neq-11,\\x\neq-5;\\\end{matrix}\right.$
$S={24}^2-4·1·(-25)=$
$= 576+100=676;$
$x_1=\frac{-24+26}{2}=\frac{2}{2}=1;$
$x_2=\frac{-24-26}{2}=-25.$
$x-25$ умові задачі не задовольняє.
Отже, $x=1,x+5=1+5=6.$
Відповідь:
$\frac{1}{6}.$
