№ 26.12 Алгебра = № 51.12 Математика
Моторний човен проплив 18 км за течією річки і 28 км проти течії за такий самий час, що й 48 км у стоячій воді. Знайдіть власну швидкість човна, якщо швидкість течії дорівнює 3 км/год.
Розв'язок:
Нехай $x$ км/год – власна швидкість човна, $x>0.$
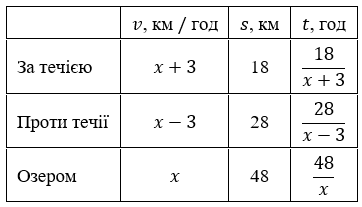
$\frac{18}{x+3}+\frac{28}{x-3}=\frac{48}{x};$
$\frac{18}{x+3}+\frac{28}{x-3}-\frac{48}{x}=0;$
$\frac{18x\left(x-3\right)+28x\left(x+3\right)-48\left(x^2-9\right)}{\left(x+3\right)\left(x-3\right)}=0;$
$\frac{18x^2-54x+28x^2+84x-48x^2+432}{x\left(x+3\right)\left(x-3\right)}=0;$
$\frac{-2x^2+30x+432}{x\left(x+3\right)\left(x-3\right)}=0;$
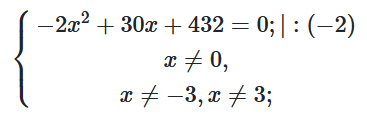
$x^2-15x-216=0;$
$D=(-15)^2-4·(-216)=$
$= 225+864=1089=33^2;$
$x_1=\frac{15+33}{2}=\frac{48}{2}=24;$
$x_2=\frac{15-33}{2}<0$ (не задовольняє умові задачі).
Відповідь:
24 км/год.
