№ 26.10 Алгебра = № 51.10 Математика
Човен, власна швидкість якого 18 км/год, проплив 40 км за течією і 16 км проти течії, витративши на весь шлях 3 год. Знайдіть швидкість течії, якщо вона менша від 4 км/год.
Розв'язок:
Нехай $x$ км/год, $x>0$ – швидкість течії річки.

$\frac{40}{18+x}+\frac{16}{18-x}=3;$
$\frac{40(18-x)+16(18+x)}{(18+x)(18-x)}=\frac{3}{1};$
$\frac{720-40x+288+16x}{(18+x)(18-x)}=\frac{3}{1};$
$\frac{1008-24x}{(18+x)(18-x)}=\frac{3}{1};$
$3\left(324-x^2\right)=1008-24x;$
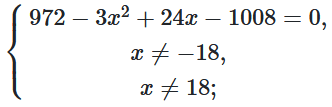
$-3x^2+24x-36=0;$
$x^2-8x+12=0;x_1=6;$
$x_2=2. $
$x=6$ умові задачі не задовольняє, оскільки $6>4.$
Відповідь:
2 км/год.
