№ 25.27 Алгебра = № 50.27 Математика
Розв’яжіть рівняння:
$\frac{1}{x-3}-\frac{14}{x^3-x^2-9x+9}=\frac{1}{x^2+2x-3}.$
Розв'язок:
$\frac{1}{x-3}-\frac{14}{x^3-x^2-9x+9}=$
$= \frac{1}{x^2+2x-3}.$
Спростимо знаменник другого і третього дробу,
тобто: $x^3-x^2-9x+9=$
$x^2(x-1)-9(x-1)=$
$= (x-1)\left(x^2-9\right)=$
$= (x-1)(x-3)·(x+3);$
$x^2+2x-3=(x+3)(x-1).$
Маємо:
$\frac{1}{x-3}-\frac{14}{(x-1)(x-3)(x+3)}=$
$= \frac{1}{(x+3)(x-1)};$
$\frac{(x-1)(x+3)-14}{(x-1)(x-3)(x+3)}=$
$= \frac{x-3}{(x-3)(x+3)(x-1)};$
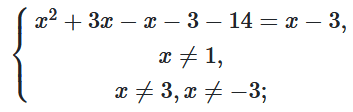
$x^2+x-14=0;$
$D=1+4·14=57;$
$D>0;$
$x_{1{,}2}=\frac{-1\pm\sqrt{57}}{2}.$
Відповідь:
$\frac{-1\pm\sqrt{57}}{2}.$
