№ 25.20 Алгебра = № 50.20 Математика
Розв’яжіть рівняння:
1. $\frac{21}{x^2-2x}-\frac{14}{x^2+2x}=\frac{5}{x};$
2. $\frac{3}{x^2-4x+4}+\frac{4}{x^2-4}+\frac{1}{x+2}=0;$
3. $\frac{5}{x^2+10x}+\frac{x+20}{x^2-10x}=\frac{10}{x^2-100};$
4. $\frac{2x+7}{x+4}-\frac{x-2}{x-1}=\frac{5}{x^2+3x-4}.$
Розв'язок:
1. $\frac{21}{x^2-2x}-\frac{14}{x^2+2x}=\frac{5}{x};$
$\frac{21}{x(x-2)}-\frac{14}{x(x+2)}-\frac{5}{x}=0;$
$\frac{21(x+2)-14(x-2)-5(x-2)(x+2)}{x(x-2)(x+2)}=0;$
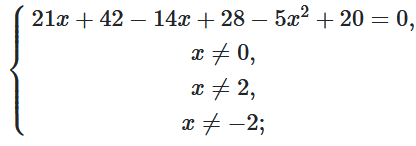
$\left\{\begin{matrix}-5x^2+7x+90=0,\\x\neq0,\\x\neq2,\\x\neq-2;\\\end{matrix}\right.$
$5x^2-7x-90=0;$
$D=(-7)^2-4·5·(-90)=$
$= 49+1800=1849=432;$
$D>0;$
$x_1=\frac{7+43}{2\cdot5}=\frac{50}{10}=5;$
$x_2=\frac{7-43}{2\cdot5}=\frac{-36}{10}=-3{,}6.$
2. $\frac{3}{x^2-4x+4}+\frac{4}{x^2-4}+\frac{1}{x+2}=0;$
$\frac{3}{(x-2)^2}+\frac{4}{(x-2)(x+2)}+\frac{1}{x+2}=0;$
$\frac{3(x+2)+4(x-2)+(x-2)^2}{(x-2)^2(x+2)}=0;$
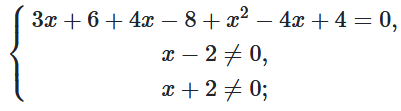
$\left\{\begin{matrix}x^2+3x+2=0,\\x\neq2,\\x\neq-2;\\\end{matrix}\right.$
$x^2+3x+2=0.$
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=-3,\\x_1x_2=2;\\\end{matrix}\right.$
звідки $\begin{matrix}x_1=-2,\\x_2=-1\\\end{matrix}$
$x_1=-2$ – не задовольняє умові.
3. $\frac{5}{x^2+10x}+\frac{x+20}{x^2-10x}=\frac{10}{x^2-100};$
$\frac{5}{x(x+10)}+\frac{x+20}{x(x-10)}=$
$= \frac{10}{(x-10)(x+10)};$
$\frac{5(x-10)+(x+20)(x+10)}{x(x+10)(x-10)}=$
$= \frac{10x}{x(x-10)(x+10)};$
$\frac{5x-50+x^2+10x+20x+200}{x(x+10)(x-10)}=$
$= \frac{10x}{x(x-10)(x+10)};$
$\left\{\begin{matrix}x^2+35x+150=0,\\x\neq0,\\x+10\neq0,\\x-10\neq0;\\\end{matrix}\right.$
$\left\{\begin{matrix}x^2+25x+150=0,\\x\neq0,\\x\neq10,x\neq-10;\\\end{matrix}\right.$
$x^2+25x+150=0.$
За теоремою Вієта:
$\left\{\begin{matrix}x_1+x_2=-25,\\x_1x_2=150\\\end{matrix}\Leftrightarrow\right.$
$\Leftrightarrow\begin{matrix}x_1=-15,\\x_2=-10;\\\end{matrix}$
$x_2=-10$ – не задовольняє умові.
Корінь рівняння $x=-15.$
4. $\frac{2x+7}{x+4}-\frac{x-2}{x-1}=\frac{5}{x^2+3x-4}.$
Врахуємо, що:
$x^2+3x-4=(x+4)(x-1).$
$x^2+3x-4=0.$
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=-3,\\x_1x_2=-4\\\end{matrix}\Leftrightarrow\right.$
$\Leftrightarrow\begin{matrix}x_1=-4,\\x_2=1.\\\end{matrix}$
Маємо:
$\frac{2x+7}{x+4}-\frac{x-2}{x-1}=\frac{5}{(x+4)(x-1)};$
$\frac{(2x+7)(x-1)-(x-2)(x+4)}{(x+4)(x-1)}=$
$= \frac{5}{(x+4)(x-1)};$
$\frac{2x^2-2x+7x-7-x^2-4x+2x+8}{(x+4)(x-1)}=$
$= \frac{5}{(x+4)(x-1)};$
$\left\{\begin{matrix}x^2+3x+1=5,\\x+4\neq0,\\x-1\neq0;\\\end{matrix}\right.$
$\left\{\begin{matrix}x^2+3x-4=5,\\x\neq-4,\\x\neq1;\\\end{matrix}\right.$
$x^2+3x-4=0;$
$\left.\begin{matrix}x_1=-4,\\x_2=1\\\end{matrix}\right\}$ – не є розв'язками рівняння.
Коренів немає.
Відповідь:
1. $-3,6;5;x\neq0;x\neq\pm2.$
2. $-1;x\neq\pm2.$
3. $-15;x\neq0;x\neq\pm10.$
4. коренів немає.
