№ 25.19 Алгебра = № 50.19 Математика
Розв’яжіть рівняння:
1. $\frac{2x-3}{x^2+4x+4}-\frac{x+1}{x^2+2x}=\frac{5}{x};$
2. $\frac{6}{x^2-9}-\frac{4}{x^2+6x+9}=\frac{1}{x-3};$
3. $\frac{6}{x^2-36}-\frac{3}{x^2+6x}=\frac{x+12}{x^2-6x};$
4. $\frac{3x+2}{x+1}+\frac{x+4}{x-3}=\frac{3x^2}{x^2-2x-3}.$
Розв'язок:
1. $\frac{2x-3}{x^2+4x+4}-\frac{x+1}{x^2+2x}=\frac{5}{x};$
$\frac{2x-3}{(x+2)^2}-\frac{x+1}{x(x+2)}=\frac{5}{x};$
$\frac{x(2x-3)-(x+1)(x+2)}{x(x+2)^2}=\frac{5(x+2)^2}{x(x+2)^2};$
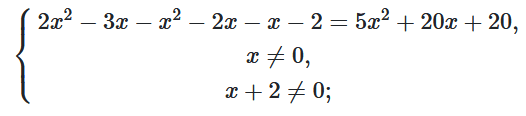
$\left\{\begin{matrix}4x^2+26x+22=0;\\x\neq0;\\x\neq-2;\\\end{matrix}\right.$
$4x^2+26x+22=0\mid:2;$
$2x^2+13x+11=0;$
$D={13}^2-4·2·11=$
$= 169-88=81=9^2;$
$D>0;$
$x_1=\frac{-13+9}{4}=\frac{-4}{4}=-1;$
$x_2=\frac{-13-9}{4}=\frac{-22}{4}=$
$= \frac{-11}{2}-5{,}5.$
2. $\frac{6}{x^2-9}-\frac{4}{x^2+6x+9}=\frac{1}{x-3};$
$\frac{6}{(x-3)(x+3)}-\frac{4}{(x+3)^2}=\frac{1}{x-3};$
$\frac{6(x+3)-4(x-3)}{(x+3)^2(x-3)}=\frac{(x+3)^2}{(x+3)^2(x-3)};$
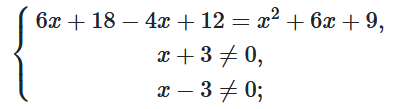
$\left\{\begin{matrix}x^2+4x-21=0,\\x\neq-3,\\x\neq3;\\\end{matrix}\right.$
$x^2+4x-21=0.$
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=-4,\\x_1x_2=-21,\\\end{matrix}\right.$
звідки $\begin{matrix}x_1=-7,\\x_2=3.\\\end{matrix}$
Отже, $\left\{\begin{matrix}x_1=-7,\\x_2=3,\\x\neq3,x\neq-3.\\\end{matrix}\right.$
Корінь рівняння $x=-7.$
3. $\frac{6}{x^2-36}-\frac{3}{x^2+6x}=\frac{x+12}{x^2-6x};$
$\frac{6}{(x-6)(x+6)}-\frac{3}{x(x+6)}=\frac{x+12}{x(x-6)};$
$\frac{6x-3(x-6)}{x(x-6)(x+6)}=\frac{(x+12)(x+6)}{x(x-6)(x+6)};$
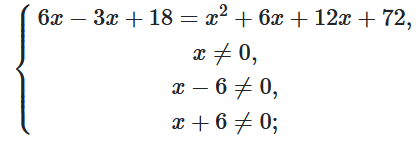
$\left\{\begin{matrix}x^2+15x+54=0,\\x\neq0,\\x\neq6,\\x\neq-6;\\\end{matrix}\right.$
$\left\{\begin{matrix}x_1=9,x_2=-6,\\x\neq0,\\x\neq6,\\x\neq-6;\\\end{matrix}\right.$
$x^2+15x+54=0.$
За теоремою Вієта:
$\left\{\begin{matrix}x_1+x_2=-15,\\x_1x_2=54\\\end{matrix}\Leftrightarrow\right.$
$\Leftrightarrow\begin{matrix}x_1=-9,\\x_2=-6.\\\end{matrix}$
Отже, корінь рівняння $x=-9.$
4. $\frac{3x+2}{x+1}+\frac{x+4}{x-3}=\frac{3x^2}{x^2-2x-3}.$
Врахуємо, що $x^2-2x-3=(x-3)(x+1).$
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=2,\\x_1x_2=-3,\\\end{matrix}\right.$
звідки $\begin{matrix}x_1=3,\\x_2=-1.\\\end{matrix}$
Тобто:
$\frac{3x+2}{x+1}+\frac{x+4}{x-3}=\frac{3x^2+1}{(x-3)(x+1)};$
$\frac{(x+1)(x-3)+(x+4)(x+1)}{(x+1)(x-3)}=$
$= \frac{3x^2+1}{(x-3)(x+1)};$
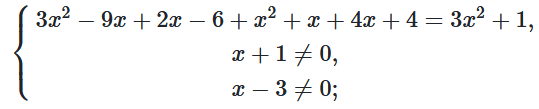
$\left\{\begin{matrix}x^2-2x-3=0,\\x\neq-1,\\x\neq3;\\\end{matrix}\right.$
$x^2-2x-3=0.$
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=2,&x_1=3,\\x_1x_2=-3,&x_2=-1\\\end{matrix}\right.$
Не задовольняють умові.
Відповідь:
1. $-1;-5{,}5;x≠0;x≠-2;$
2. $–7;$
3. $-9;x\neq0;x\neq\pm6;$
4. розв'язків немає.
