Завдання № 25.15

№ 25.15 Алгебра =  № 50.15 Математика

Розв’яжіть рівняння:

1. $\frac{x^4-10x^2+9}{x+3}=0;$ 

2. $\frac{6x^2+19x-7}{1-3x}=5;$ 

3. $\frac{2x^2-5x+2}{x^2-4}=3;$ 

4. $\frac{4x+2}{1+2x}=6x+5.$ 

Розв'язок:

1. $\frac{x^4-10x^2+9}{x+3}=0;$

$\left\{\begin{matrix}x^4-10x+9=0,\\x+3\neq0,x\neq3;\\\end{matrix}\right.$

$x^4-10x^2+9=0.$ 

Заміна: $x^2=t,t\geq.$ 

$t^2-10t+9=0. $

За теоремою Вієта маємо:

$\left\{\begin{matrix}t_1+t_2=10,\\t_1t_2=9,\\\end{matrix}\right.$ 

звідки $\begin{matrix}t_1=9,\\t_2=1.\\\end{matrix}$ 

Обернена заміна: $\left\{\begin{matrix}x^2=9,\\x^2=1\\\end{matrix}\Leftrightarrow\left\{\begin{matrix}x=\pm3,\\x\neq\pm1.\\\end{matrix}\right.\right.$ 

Отже, $\left\{\begin{matrix}x_{1,2}=\pm3,\\x_{3,4}=\pm1,\mathrm{\ \ } \\x\neq-3.\\\end{matrix}\right.$ 

корені рівняння: $\left\{\begin{matrix}x_1=3,\\x_{2,3}=\pm1,\\x\neq-3.\\\end{matrix}\right.$ 

2. $\frac{6x^2+19x-7}{1-3x}=5;$

$\left\{\begin{matrix}6x^2+19x-7=5(1-3x),\\1-3x\neq0;\\\end{matrix}\right.$

$\left\{\begin{matrix}6x^2+19x-7=5-15x,\\x\neq\frac{1}{3};\\\end{matrix}\right.$

$6x^2+34x-12=0\mid:2;$

$3x^2+17x-6=0;$

$D={17}^2-4·3·(-6)=$

$= 289+72=361=192;$

$D>0;$

$x_1=\frac{-17+19}{6}=\frac{2}{6}=\frac{1}{3};$

$x_2=\frac{-17-19}{6}=\frac{-36}{6}=-6.$

Отже, $\left\{\begin{matrix}x_1=\frac{1}{3},\\x_2=-6,x=-6\mathrm{\ } \\x\neq\frac{1}{3},\\\end{matrix}\right.$ - корінь рівняння. $x≠13,$

3. $\frac{2x^2-5x+2}{x^2-4}=3;$

$\left\{\begin{matrix}2x^2-5x+2=3\left(x^2-4\right),\\x^2-4\neq0;\\\end{matrix}\right.$

$\left\{\begin{matrix}2x^2-5x+2=3x^2-12,\\x\neq\pm2;\\\end{matrix}\right.$ 

$\left\{\begin{matrix}x^2+5x-14=0,\\x\neq\pm2;\\\end{matrix}\right.$

$x^2+5x-14=0.$

За теоремою Вієта маємо:

$\left\{\begin{matrix}x_1+x_2=-5,\\x_1x_2=-14,\\\end{matrix}\right.$

звідки: $\left\{\begin{matrix}x_1=-7,\\x_2=2.\\\end{matrix}\right.$

Отже, $\left\{\begin{matrix}x_1=-7,\\x_2=2,\\x\neq\pm2.\\\end{matrix}\right.$

Корінь рівняння $x=-7.$

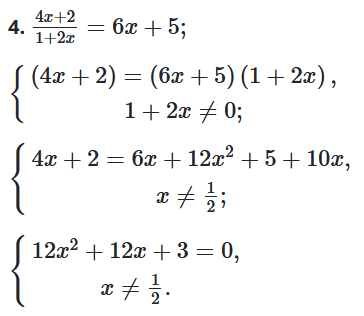
$12x^2+12x+3=0\mid:3;$

$4x^2+4x+1=0;$

$(2x+1)^2=0; 2x+1=0;$

$ x=-\frac{1}{2}.$

Отже,$x=-12,x≠-12.$

Коренів немає.

Відповідь: 

1. $3;\pm1;x\neq-3;$

2. $-6;x\neq\frac{1}{3};$

3. $-7;x\neq\pm2;$

4. коренів немає.