№ 25.13 Алгебра = № 50.13 Математика
Розв’яжіть рівняння:
1. $\frac{20}{x}-\frac{20}{x+1}=1;$
2. $\frac{2}{x}-\frac{1}{x-2}=1.$
Розв'язок:
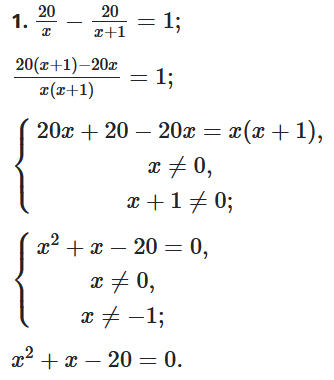
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=-1,\\x_1x_2=-20\\\end{matrix}\Leftrightarrow\begin{matrix}x_1=-5,\\x_2=4,\\\end{matrix}\right.$
тобто
$\left\{\begin{matrix}x_1=-5,\\x_2=4,\\x\neq0,x\neq-1;\\\end{matrix}\right.$
2. $\frac{2}{x}-\frac{1}{x-2}=1;$
$\frac{2\left(x-2\right)+x}{x\left(x-2\right)}=1;$
$\left\{\begin{matrix}2x-4+x=x(x-2),\\x\neq0,\\x-2\neq0;\\\end{matrix}\right.$
$\left\{\begin{matrix}x^2-2x-3x+4=0,\\x\neq0,\\x\neq2;\\\end{matrix}\right.$
$x^2-5x+4=0. $
За теоремою Вієта маємо:
$\left\{\begin{matrix}x_1+x_2=5,\\x_1x_2=4\\\end{matrix}\Leftrightarrow\begin{matrix}x_1=4,\\x_2=1,\\\end{matrix}\right.$
тобто $\left\{\begin{matrix}x_1=4,\\x_2=1,\\x\neq0,\\x\neq2.\\\end{matrix}\right.$
Відповідь:
1. $–5; 4; $
2. $–4; 3.$
