№ 24.32 Алгебра = № 49.32 Математика
Побудуйте графік функції:
1. $y=\frac{x^2+x-2}{x-1};$
2. $y=\frac{x^3-2x^2-3x}{x^2+x}.$
Розв'язок:
1. Спростимо вираз:
$\frac{x^2+x-2}{x-1}=$
$= \frac{(x-1)(x+2)}{(x-1)}=x+2.$
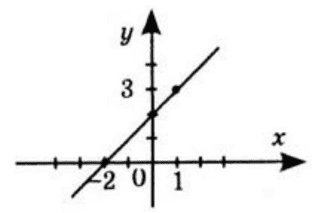
Маємо: $y=x+2,x\neq1$ – пряма,
якщо $x=0,$ то $y=2,$
якщо $y=0,$ то $x=-2.$
$y=x+2$
2. Спростимо вираз:
$\frac{x^3-2x^2-3x}{x^2+x}=$
$= \frac{x\left(x^2-2x+3\right)}{x(x+1)}=$
$= \frac{(x-3)(x+1)}{(x+1)}=x-3.$
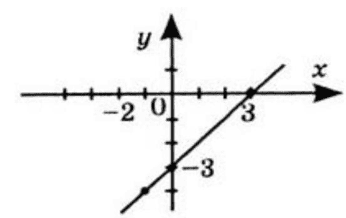
Маємо $y=x-3,x\neq1,x\neq-1.$
Якщо $x=0,$ то $y=-3;$
якщо $y=0,$ то $x=3.$
$y=x-3$
Відповідь:
1. $(1; 3);$
2. $(0; –3); (–1; –4).$
