Завдання № 23.7

№ 23.7 Алгебра =  № 43.7 Математика

Знайдіть площу прямокутника, якщо сума двох його непаралельних сторін дорівнює 14 см, а діагональ дорівнює 10 см.

Розв'язок:

Нехай $AC=10$см,$AB=x,BC=14-x.$

 
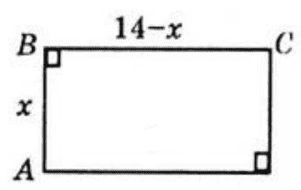
За теоремою Піфагора

$AB^2+BC^2=AC^2;$

$ x^2+\left(14-x^2\right)={10}^2;$

$x^2+196-28x+x^2-100=$

$= 0;$

$2x^2-28x+96=0;$

$x^2-14x+48=0;$

$D=(-14)^2-4·48=$

$= 196-192=4;D=2;$

$x_1=\frac{14+2}{2}=\frac{16}{2}=8;$

$x_2=\frac{14-2}{2}=\frac{12}{2}=6.$

$14-x=14-8=6$ або 

$14-x=14-6=8;$ 

$S=6·8=48$ см².

Відповідь:

48 см².