№ 23.6 Алгебра = № 43.6 Математика
Один з катетів прямокутного трикутника на 7 см менший від другого. Знайдіть периметр трикутника, якщо його гіпотену за дорівнює 13 см.
Розв'язок:
Нехай $AC=x,$ тоді $BC=x-7.$
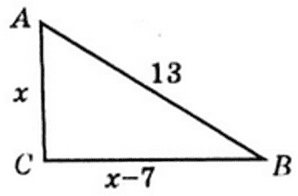
За теоремою Піфагора
$AC^2+BC^2=AB^2;$
$x^2+(x-7)^2={13}^2;$
$x^2+x^2-14x+49-169=0;$
$2x^2-14x-120=0;$
$x^2-7x-60=0;x_1=12;$
$x_2=-5<0$ (умові задачі не задовольняє).
$x-7=12-7=5;$
$P=12+5+13=$
$= 25+5=30$ (см).
Відповідь:
30 см.
