Завдання № 23.15

№ 23.15 Алгебра =  № 43.15 Математика

Периметр прямокутника дорівнює 44 см, а сума площ квадратів, побудованих на сусідніх сторонах, дорівнює 244 см². Знайдіть сторони прямокутника.

Розв'язок:

Нехай $CD=x,$ тоді $BC=22-x.$

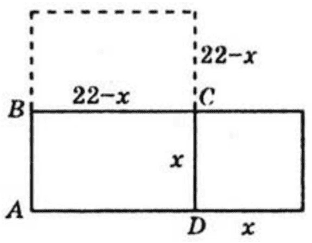
$x^2+(22-x)^2=244;$

$x^2+484-44x+x^2=244;$

$x^2+484-44x+x^2-244=$

$= 0;$

$2x^2-44x+240=0;$

$x^2-22x+120=0;$

$D=(-22)^2-4·1·120=$

$= 484-480=4;$

$\sqrt D=4;$

$x_1=\frac{22+2}{2}=\frac{24}{2}=12;$

$x_2=\frac{22-2}{2}=\frac{20}{2}=10;$

$22-x=22-12=10$ або

$22-x=22-10=12.$

Відповідь:

10 см і 12 см.