№ 23.14 Алгебра = № 43.14 Математика
Дві дороги перетинаються під прямим кутом. Від перехрестя доріг одночасно рушили два велосипедисти, один у східному напрямку, другий – у північному. Швидкість першого була на4 км/год більшою за швидкість другого. Через 2 год відстань між ними становила 40 км. Якою була швидкість кожного з велосипедистів?
Розв'язок:
Нехай швидкість другого велосипедиста $x$ км/год, тоді швидкість першого -$(x+4)$ км / год. AB=40 км.
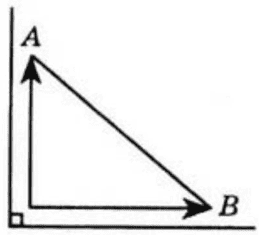
$(2x)^2+(2(x+4))^2={40}^2;$
$4x^2+(2x+8)^2=1600;$
$4x^2+4x^2+32x+$
$+ 64-1600=0;$
$8x^2+32x-1536=0\mid:8;$
$x^2+4x-192=0;$
$D=4^2-4·1·(-192)=$
$= 16+768=784;$
$\sqrt D=28;$
$x_1=\frac{-4+28}{2}=\frac{24}{2}=12;$
$x_2=\frac{-4-28}{2}<0$(умові задачі не задовольняє).
$x+4=12+4=16$ (км/год).
Відповідь:
12 км/год; 16 км/год.
