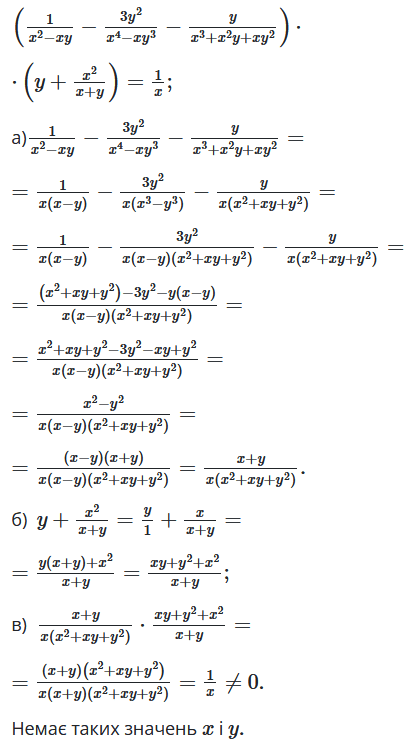ВПР 1 №65 Алгебра = ВПТ 3 №28 Математика
Чи може значення виразу
$(\frac{1}{x^2-xy} − \frac{3y^2}{x^4-xy^3} − \frac{y}{x^3+x^2y+xy^2})\cdot$
$\cdot(y + \frac{x^2}{x+y})$
для деяких значень змінних x і y дорівнювати нулю?
Розв'язок:
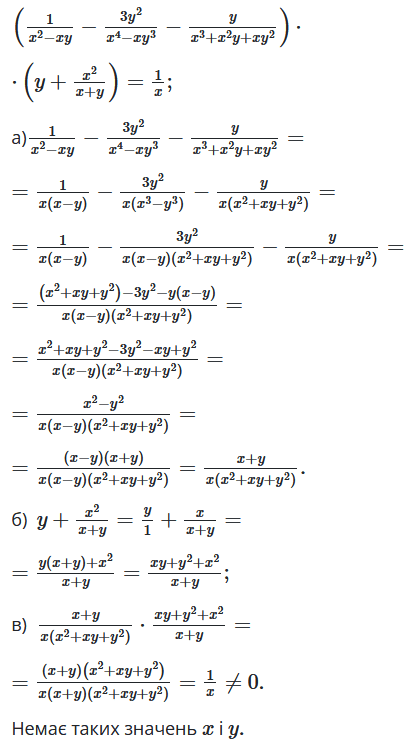
ВПР 1 №65 Алгебра = ВПТ 3 №28 Математика
$(\frac{1}{x^2-xy} − \frac{3y^2}{x^4-xy^3} − \frac{y}{x^3+x^2y+xy^2})\cdot$
$\cdot(y + \frac{x^2}{x+y})$