№ 2.25 Алгебра = № 2.25 Математика
Знайдіть область визначення функції та побудуйте її графік:
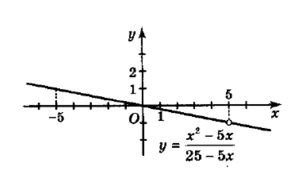
$1) y = \frac{x^2\ -\ 5x\ }{25\ -\ 5x}$;
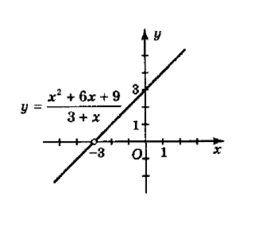
$2) y = \frac{x^2\ +\ 6x\ +\ 9}{3\ +\ x}$.
Розв'язок:
1) Спростимо вираз:
$\frac{x^2\ -\ 5x\ }{25\ -\ 5x} = \frac{x(x\ -\ 5)\ }{-5(x\ -\ 5)} = −\frac{x\ }{5}.$
Тобто маємо $y = −\frac{x }{5},$ x ≠ 5.
Якщо x = 5, то y = −1.
2) Спростимо вираз:
$\frac{x^2\ +\ 6x\ +\ 9}{3\ +\ x} = \frac{{(x\ +\ 3)}^2\ }{x\ +\ 3} = x + 3.$
Тобто маємо y = x + 3, x ≠ −3.
| y = x + 3 | ||
| x | 0 | −3 |
| y | 3 | 0 |
Відповідь:
1) (5; −1);
2) (−3; 0).