ВПР 4 №27 Геометрія = ВПТ 10 №27 Математика
CK – медіана рівнобедреного трикутника ABC з основою AB. На цій медіані вибрано деяку точку M. Доведіть, що SAMC = SBMC.
Розв'язок:
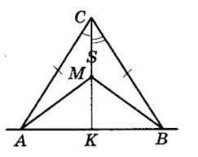
У ΔABC AC = BC.
Медіана CK є бісектрисою кута C: ∠ACM = ∠BCM.
Тоді ΔAMC = ΔBMC (за двома сторонами і кутом між ними (CM — спільна сторона)).
Оскільки рівні фігури мають рівні площі, то SΔAMC = SΔBMC.
