ВПР 4 №15 Геометрія = ВПТ 10 №15 Математика
У прямокутний трикутник ABC (∠C = 90°) вписано квадрат MNKL так, що точки N і K належать гіпотенузі (причому N лежить між A і K), M належить AC, L належить BC. AN = m, KB = n. Знайдіть площу квадрата.
Розв'язок:
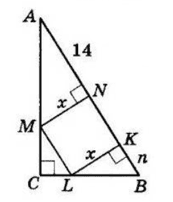
Позначимо сторону квадрата x.
$ΔAMN$ і $ΔLBK$ — прямокутні.
$∠AMN = 90° – ∠A,$
$ ∠B = 90° – ∠A.$
Тоді $ΔAMN ~ ΔLBK$ за двома кутами, тому
$\frac{AN}{MN}\ =\ \frac{LK}{KB};$
$\frac{m}{x}\ =\ \frac{x}{n};$
$x^2 = mn.$
$S_{MNKL} = x^2,$ отже,
$S_{MNKL} = nm.$
Відповідь:
$nm.$
