Завдання № 25.31

№ 25.31 Геометрія =  № 48.31 Математика

Точка дотику кола, вписаного в прямокутну трапецію, ділить більшу бічну сторону на відрізки 1 см і 4 см. Знайдіть площу трапеції.   

Розв'язок:

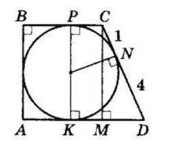
$ABCD$ — трапеція $(BC || AD), ∠A = ∠B = 90°.$

Проведемо висоти $PK$ (через центр вписаного кола) і $CM.$ 

$ON ⊥ CD$ — радіус, проведений в точку дотику, $CM = 1$ см, $ND = 4$ см.

За властивістю дотичних, проведених з однієї точки до кола, 

$CN = PC = 1$ см,

$KD = ND = 4$ см. 

$PCMK$ — прямокутник

$(PK || CM, PK = CM,$

$ ∠K = 90°),$

тоді $KM = PC = 1$ см. 

$MD = KD − KM =$

$= 4 − 1 = 3$ (см).

З $∆CMK\ CM =$

$= \sqrt{CD^2 - MD^2} =$

$=  \sqrt{5^2 - 3^2} =$

$= \sqrt{25\ -\ 9} = \sqrt{16} = 4$ (см).

$PK = CM = 4$ см, 

$ON = \frac{1}{2} PK = 2$ см (як радіуси).

$AK = BP = 2$ см.

$BC = BP + PC =$

$= 2 + 1 = 3$ (см);

$AD = 2 + 4 = 6$ (см).

$S_{\Delta ABCD}\ =\ \frac{BC\ +\ AD}{2}· CM =$

$= \frac{3 + 6}{2} · 4 = 18$ (см²).

Відповідь:

$18$ см².