№ 24.15 Геометрія = № 47.15 Математика
У прямокутнику ABCD BD = 10 см. Вершина B віддалена від прямої AC на 3 см. Знайдіть площі трикутника ABC і прямокутника ABCD.
Розв'язок:
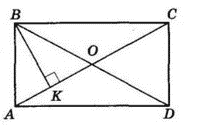
$AC = BD = 10$ см як діагоналі прямокутника.
$BK ⊥ AC$ — відстань від вершини $B$ до прямої $AC, BK = 3$ см.
$S_{\Delta ABC}\ =\ \frac{1}{2}\ AC\ · BK =$
$= \ \frac{1}{2} · 10 · 3 = 15$ (см2).
$ΔABC = ΔCDA$ за двома катетами.
$S_{ABCD} = 2S_{ΔABC} = 2 · 15 =$
$= 30$ (см2).
Відповідь:
$15$ см2, $30$ см2.
