№ 24.13 Геометрія = № 47.13 Математика
1. Діагоналі ромба дорівнюють 8 см і 10 см. Знайдіть площу ромба.
2. Використовуючи формулу площі прямокутного трикутника, виведіть формулу площі ромба через його діагоналі d1 і d2.
Розв'язок:
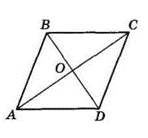
$ABCD$ — ромб, $AC$ і $BD$ — діагоналі.
1. $AC = 10$ см, $BD = 8$ см.
$S_{ABCD}=S_{\Delta ABC}+\ S_{\Delta ADC} =$
$= \ \frac{1}{2} AC · BO + \ \frac{1}{2} DO · AC =$
$= \ \frac{1}{2} AC (BO + DO) =$
$= \ \frac{1}{2}AC · BD =$
$= \ \frac{1}{2} · 10 · 8 = 40$ (см2).
2. $AC = d_1, BD = d_2.$
$S_{ABCD}= S_{\Delta ABC} + S_{\Delta ADC} =$
$= \ \frac{1}{2} AC · BO + \frac{1}{2} DO · AC =$
$= \ \frac{1}{2} AC (BO + DO) =$
$ \ \frac{1}{2} AC · BD = 12 d_1d_2.$
Відповідь:
1. $40$ см2;
2. $\frac{1}{2} d_1d_2.$
