№ 22.17 Геометрія = № 45.17 Математика
Периметр прямокутника 26 см, а одна з його сторін на 5 см більша за другу. Знайдіть сторону квадрата, що має таку саму площу, як і прямокутник.
Розв'язок:
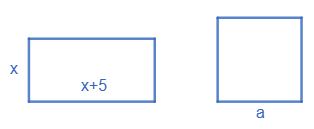
Нехай одна сторона прямокутника $x$ см, а друга — $(x + 5)$ см.
Тоді його периметр $2(x + x + 5),$ що за умовою дорівнює $26$ см:
$2(2x + 5) = 26;$
$4x + 10 = 26; $
$4x = 16;$
$x = 4.$
Отже, сторони прямокутника дорівнюють $4$ см і $4 + 5 = 9$ (см).
$S_{пр} = 4 · 9 = 36$ (см).
Площа квадрата $S_{кв} = S_{пр} = 36$ см2.
Сторона квадрата $a = \sqrt{36} = 6$ (см).
Відповідь:
$6$ см.
