Завдання № 22.15

№ 22.15 Геометрія =  № 45.15 Математика

Знайдіть площу квадрата, діагональ якого дорівнює:

1. 8 см;  
2. d см.  

Розв'язок:

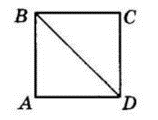
$S_{ABCD} = AB^2. $

З $ΔABD\ BD^2 = $

$= AB^2 + AD^2 = 2AB^2;$

$AB^2\ = \frac{BD^2}{2};$

$ AB = \sqrt{\frac{BD^2}{2}} = \frac{BD}{\sqrt2}$ (см).

1. $ AB\ =\ \frac{8}{\sqrt2}\ =\ \frac{8\sqrt2}{\sqrt2}\ =\ 4\sqrt2$ (см).

$S_{ABCD} = (4\sqrt2)^2 = 16 · 2 =$

$= 32$ (см²).

2. $AB\ =\ \frac{d}{\sqrt2}$ (см).

$S_{ABCD}\ =\ (\frac{d}{\sqrt2})^2 = \frac{d^2}{2}$  (см²).

Відповідь:

1. 32 см²;

2. $\frac{d^2}{2}$ см².