ДСР 4 Геометрія = ДСР 8 Математика
З точки до прямої проведено дві похилі, різниця довжин яких дорівнює 1 см. Знайдіть довжину меншої похилої, якщо проекції похилих дорівнюють 4 см і 7 см.
А. $15$ см;
Б. $16$ см;
В. $17$ см;
Г. $18$ см.
Розв'язок:
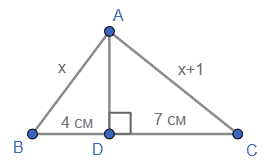
1. $BD = 4$ см; $DC = 7$ см.
$BD < DC,$ тому $AB < AC.$
2. Позначимо $AB = x$ см,
тоді $AC = x + 1$ (см).
3. Маємо у $△ABD: AD^2 = x^2 – 4^2;$
а у $△ADC: AD^2 =$
$= (x + 1)^2 − 7^2.$
4. Тоді $x^2 – 16 = x^2 + 2x + 1 – 49;$
$2x = 32;$
$x = 16.$
Відповідь:
Б. $16$ см.
