№ 20.23 Геометрія = № 39.23 Математика
Аркуш паперу склали вчетверо так, що отримали прямокутник зі сторонами вдвічі меншими, ніж сторони аркуша. Потім отриманий прямокутник прокололи у двох місцях, аркуш розгорнули й через кожні дві отримані точки (проколу) провели пряму. Яку найменшу і яку найбільшу кількість прямих при цьому можна отримати?
Розв'язок:
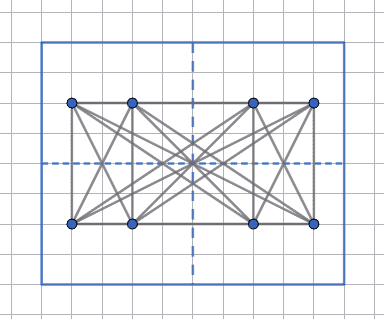
1. Найменшу кількість прямих отримаємо, якщо проколи зробити так, що вони лежать на прямій, паралельній стороні прямокутника. В цьому випадку після розгортання ми отримаємо 8 точок, розміщених у два ряди.
З'єднавши кожну точку першого ряду з кожною точкою другого ряду, отримаємо 4 · 4 = 16 прямих. І ще дві прямі проходять через кожну з четвірок точок.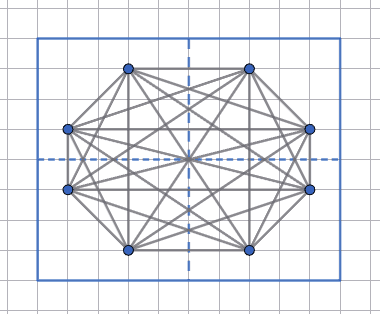
2. Якщо проколи не лежать на прямій, паралельній стороні многокутника, то на розгорнутому аркуші проколи утворюють опуклий восьмикутник. Кожна з 8 точок утворює пару, через яку проведено пряму, з кожною з решти семи точок.
Всього 7 · 8 = 56 пар. Оскільки порядок в парі не суттєвий, то пари, наприклад, 1–а і 3–я та 3–я і 1–а точки — це та сама пара. Таким чином, найбільша можлива кількість прямих 56 : 2 = 28.
Відповідь:
1. 18 прямих;
2. 28.
