№ 20.11 Геометрія = № 39.11 Математика
За двома катетами трикутника ABC (∠C = 90°) знайдіть його гіпотенузу та гострі кути з точністю до хвилини:
1. $AC = 4$ см; $BC = 4\sqrt{3}$ см;
2. $AC = 8$ дм; $BC = 15$ дм;
3. $AC = 3$ см; $BC = 9$ см;
4. $AC = 7 m$ дм; $BC = 24 m$ дм.
Розв'язок:
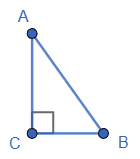
1. $АВ = \sqrt{AC^2+ BC^2} =$
$= \sqrt{4^2+(4\sqrt3)^2} = $
$= \sqrt{16+48} = \sqrt{64} = 8$ (см).
$tg ∠A = \frac{BC}{AC} = \frac{4\sqrt3}{4} = \sqrt3;$
∠A = 60°.
∠B = 90° – ∠A =
= 90° – 60° = 30°.
2. $AB = \sqrt{AC^2+ BC^2} = $
$= \sqrt{8^2+ 15^2} =$
$= \sqrt{64+ 225} = \sqrt{289} = 17$ (дм).
$tg ∠A = \frac{BC}{AC} = \frac{15}{8} = 1{,}875;$
∠A = 61°56'.
∠B = 90° – ∠A = 90° – 61°56' =
= 28°4'.
3. $AB = \sqrt{AC^2+ BC^2} = $
$= \sqrt{3^2+ 9^2} = \sqrt{9+ 81}= $
$= \sqrt{90} = 3\sqrt{10}$ (см).
$tg\ \angle A\ =\ \frac{BC}{AC}\ =$
$\ \frac{9}{3}\ =\ 3;\ \angle A\ =\ 71°34'.$
∠B = 90° – 71°34' = 18°26'.
4. $AB = \sqrt{AC^2+ BC^2}= $
$ = \sqrt{7m^2+ 24m^2} =$
$\sqrt{49m^2+ 576m^2} = $
$= \sqrt{625m^2} = 25m$ (дм).
$tg ∠A = \frac{BC}{AC} = \frac{24m}{7m} = 3{,}429;$
∠A = 73°44'. ∠B = 16°16'.
Відповідь:
1. 8 см, 60°, 30°.
2. 17 дм, 61°56', 28°4'.
3. $3\sqrt{10}$ см, 71°34', 18°26'.
4. 25m дм, 73°44', 16°16'.
