№ 19.43 Геометрія = № 38.43 Математика
Катет прямокутного трикутника дорівнює 12 см, а його проекція на гіпотенузу – 7,2 см. Знайдіть периметр трикутника.
Розв'язок:
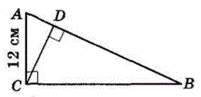
У $ΔABC ∠C = 90°, AC = 12$ см.
Проведемо $CD ⊥ AB.$
Тоді $AD = 7{,}2$ см — проекція катета $AC$ на гіпотенузу $AB.$
За властивістю катета:
$AC^2 = AD · AB;$
$AB = AC^2 : AD =$
$= 12^2 : 7{,}2 = 20$ (см).
З $ΔABC\ BC =$
$= \sqrt{AB^2 - AC^2} =$
$= \sqrt{20^2 - 12^2} =$
$= \sqrt{400\ -\ 144} =$
$= \sqrt{256} = 16$ (см).
$P_{ΔABC} = 12 + 20 + 16 = 48$ (см).
Відповідь:
$48$ см.
