№ 18.8 Геометрія = № 37.8 Математика
Точка лежить на відстані 6 см від прямої. Із цієї точки до прямої проведено похилу, що утворює з прямою кут 30°. Знайдіть довжину похилої та її проекції на пряму.
Розв'язок:
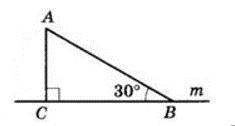
$AC ⊥ m$ — відстань від точки $A$ до прямої $m.$
$AC = 6$ см. $AB$ — похила,
$∠ABC = 30°.$
За властивістю катета, що лежить проти кута $30°$
$AC\ =\ \frac{1}{2}AB.$
$AB = 2AC = 2 · 6$ см $= 12$ см.
З $ΔABC\ BC =$
$= \sqrt{AB^2 - AC^2} =$
$= \sqrt{12^2 - 6^2} =$
$= \sqrt{(12\ -\ 6)(12\ +\ 6)} =$
$ = \sqrt{6 · 18} = 6\sqrt3$ (см).
Відповідь:
$6\sqrt3$ см.
