№ 17.30 Геометрія = № 36.30 Математика
Катети прямокутного трикутника відносяться як 7 : 24, а гіпотенуза дорівнює 50 см. Знайдіть периметр трикутника.
Розв'язок:
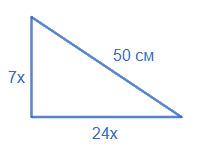
Нехай катети $a = 7x$ см, $b = 24x$ см, гіпотенуза $c = 50$ см.
$a^2 + b^2 = c^2;$
$(7x)^2 + (24x)^2 = 50^2;$
$49x^2 + 576x^2 = 2500;$
$625x^2 = 2500;$
$x^2 = 4;$
$x = 2.$
$a = 7 · 2 = 14$ (см);
$b = 24 · 2 = 48$ (см).
$P_Δ = a + b + c = $
$= 14 + 48 + 50 = 112$ (см).
Відповідь:
$112$ см.
