№ 17.18 Геометрія = № 36.18 Математика
Катети прямокутного трикутника дорівнюють 7 см і 8 см. Знайдіть довжину медіани, проведеної до більшого катета.
Розв'язок:
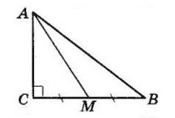
У $ΔABC, ∠C = 90°,$
$ AC = 7$ см, $BC = 8$ см.
$AM$ — медіана.
Тоді $CM = BM = \frac{1}{2}BC =$
$= \frac{1}{2} · 8 = 4$ (см).
У $ΔAMC, ∠C = 90°,$
$AM = \sqrt{AC^2 + CM^2} =$
$= \sqrt{7^2 + 4^2} = \sqrt{49\ +\ 16} =$
$= \sqrt{65}$ (см).
Відповідь:
$\sqrt{65}$ см.