ВПР 2 №8 Геометрія = ВПТ 6 №8 Математика
У трикутнику проведено середню лінію. Чи подібний трикутник, що утворився, даному трикутнику?
Розв'язок:
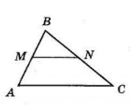
У ΔABC M — середина AB, N — середина BC.
Тоді MN — середня лінія,
MN = $\frac{1}{2}AC.$
У трикутниках ABC і MBN
∠B — спільний,
∠BMN = ∠BAC,
∠BNM = ∠BCA як відповідні (MN||AC).
MB = $\frac{1}{2}$AB,
NB = $\frac{1}{2}$BC,
MN = $\frac{1}{2}$AC.
Отже, ΔABC ~ ΔMBN за означенням, бо їх відповідні кути рівні, а відповідні сторони пропорційні.
