ДСР 3 Геометрія = ДСР 6 Математика
CL – бісектриса трикутника ABC. AC = 6 см, BC = 9 см. Більший з відрізків, на які бісектриса CL ділить сторону AB, дорівнює 3 см. Знайдіть AB.
A. 7,5 см;
Б. 6 см;
В. 5 см;
Г. 6,5 см.
Розв'язок:
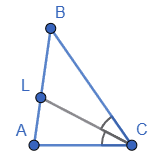
1. $\frac{AC}{BC}=\ \frac{AL}{LB}.$
2. Оскільки AC < BC, то AL < LB.
За умовою LB = 3 (см).
3. Маємо $\frac{6}{9}=\ \frac{AL}{3};$
9AL = 18; AL = 2 (см).
4. Тоді AB = AL + LB = 2 + 3 = 5 (см).
Відповідь:
В. 5 см.
