№ 16.29 Геометрія = № 28.29 Математика
На продовженні найбільшої сторони AC трикутника ABC відкладено відрізок CM = BC. Чи може кут ABM бути:
1. гострим;
2. прямим?
Розв'язок:
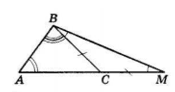
∠BCM = ∠A + ∠B за властивістю зовнішнього кута трикутника.
ΔBCM — рівнобедрений за побудовою (BC = CM).
Тому:
∠CBM = ∠BMC = $\frac{180° - ∠BCM}{2}$ =
= $\frac{180° - (∠A + ∠B)}{2}$;
∠ABM = ∠B + ∠CBM =
= ∠B + $\frac{180° - (∠A + ∠B)}{2}$ =
= $\frac{2∠B + 180° - ∠A - ∠B}{2}$ =
= $\frac{180° +∠B - ∠A}{2}$ = 90° + $\frac{∠B - ∠A}{2}$.
Оскільки за умовою у ΔABC сторона AC найбільша, то і ∠B — найбільший.
Отже, ∠B − ∠A > 0.
Таким чином, ∠ABM не може бути ні гострим, ні тупим, бо
90° + $\frac{∠B - ∠A}{2}$.
Відповідь:
1. ні;
2. ні.
