№ 14.25 Геометрія = № 26.25 Математика
У рівнобічній трапеції діагональ ділить гострий кут навпіл. Доведіть, що тупий кут трапеції дорівнює тупому куту між діагоналями.
Розв'язок:
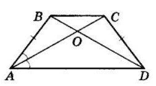
ABCD — трапеція, AD || BC, AB = CD;
O — точка перетину діагоналей ∠BAC = ∠CAD.
Позначимо для зручності ∠BAC = ∠CAD = α.
Тоді:
∠A = 2α.
∠B = 180° − ∠A = 180° − 2α.
∠BCA = ∠CAD = α, як внутрішні різносторонні при паралельних прямих BC і AD і січній AC.
У ΔCBO ∠CBO = ∠BCO = α, кути при основі рівнобедреного трикутника.
∠BOC = 180° − (∠CBO + ∠BCO) = 180° − 2α.
Отже, ∠ABC=∠BOC.
