№ 12.15 Геометрія = № 24.15 Математика
Доведіть, що точка перетину бісектрис кутів трапеції, прилеглих до бічної сторони, належить середній лінії трапеції.
Розв'язок:
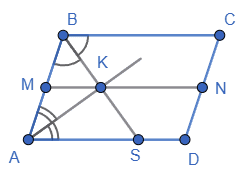
Нехай бісектриса кута ABC перетинає сторону AD у точці S. Тоді ΔABS – рівнобедрений з основою BS (∠CBS = ∠BSA як внутрішні різносторонні при паралельних прямих BC і AD і січній BS, тоді ∠ABS = ∠BSA, AB = AS).
Значить, його бісектриса AK є також медіаною, тобто K – середина BS.
Якщо MN – середня лінія трапеції, то MN || AD. Оскільки M і K – середини сторін AB і BS, то MK – середня лінія ΔABS і MK || AS.
Оскільки через точку M можна провести лише одну пряму, паралельну даній, то точка K лежить на середній лінії трапеції.
